后缀自动机(SAM)
后缀自动机
1. 后缀自动机实现的功能
给定一个string,例如为“aabab”他有后缀b, ab, bab等,需要把他们构建在同一个trie上,如果暴力地构建得到以下trie结构
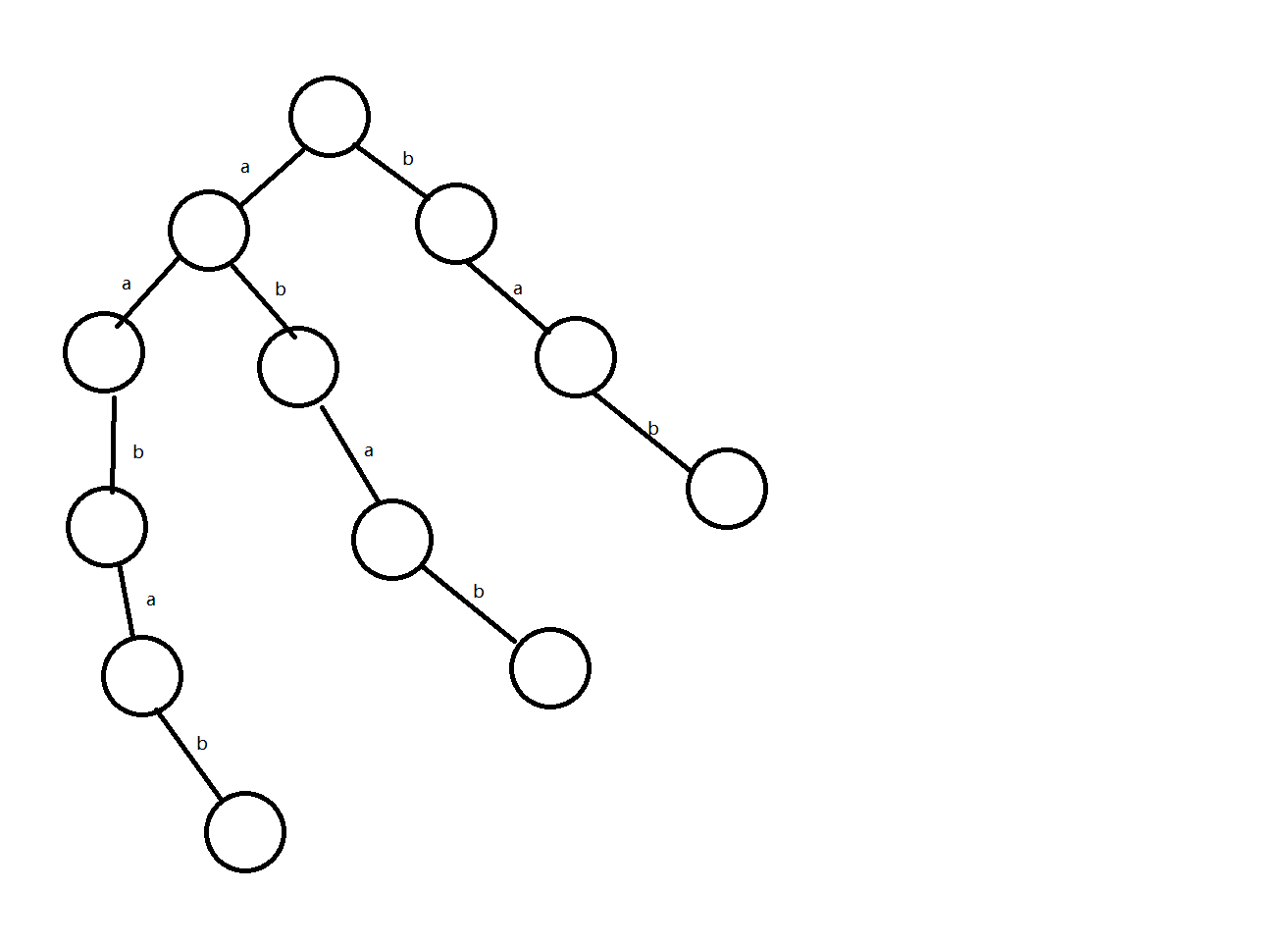
如上图所示,但是我们会发现一个问题,节点个数有 $O(n^2)$个,但是我们可以发现
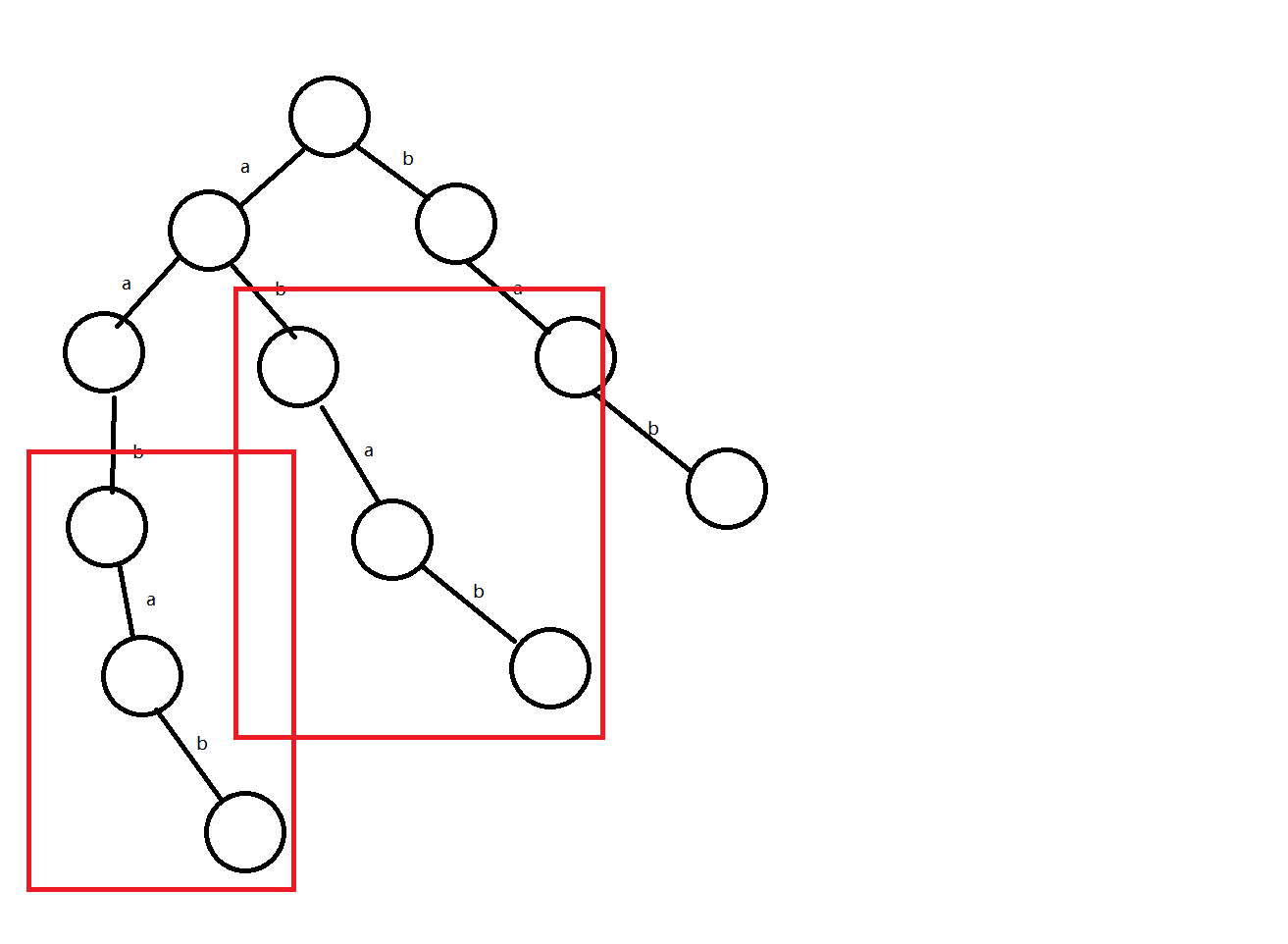
两个红色矩形内代表的后缀子串都是bab,因此可以化简为以下形式
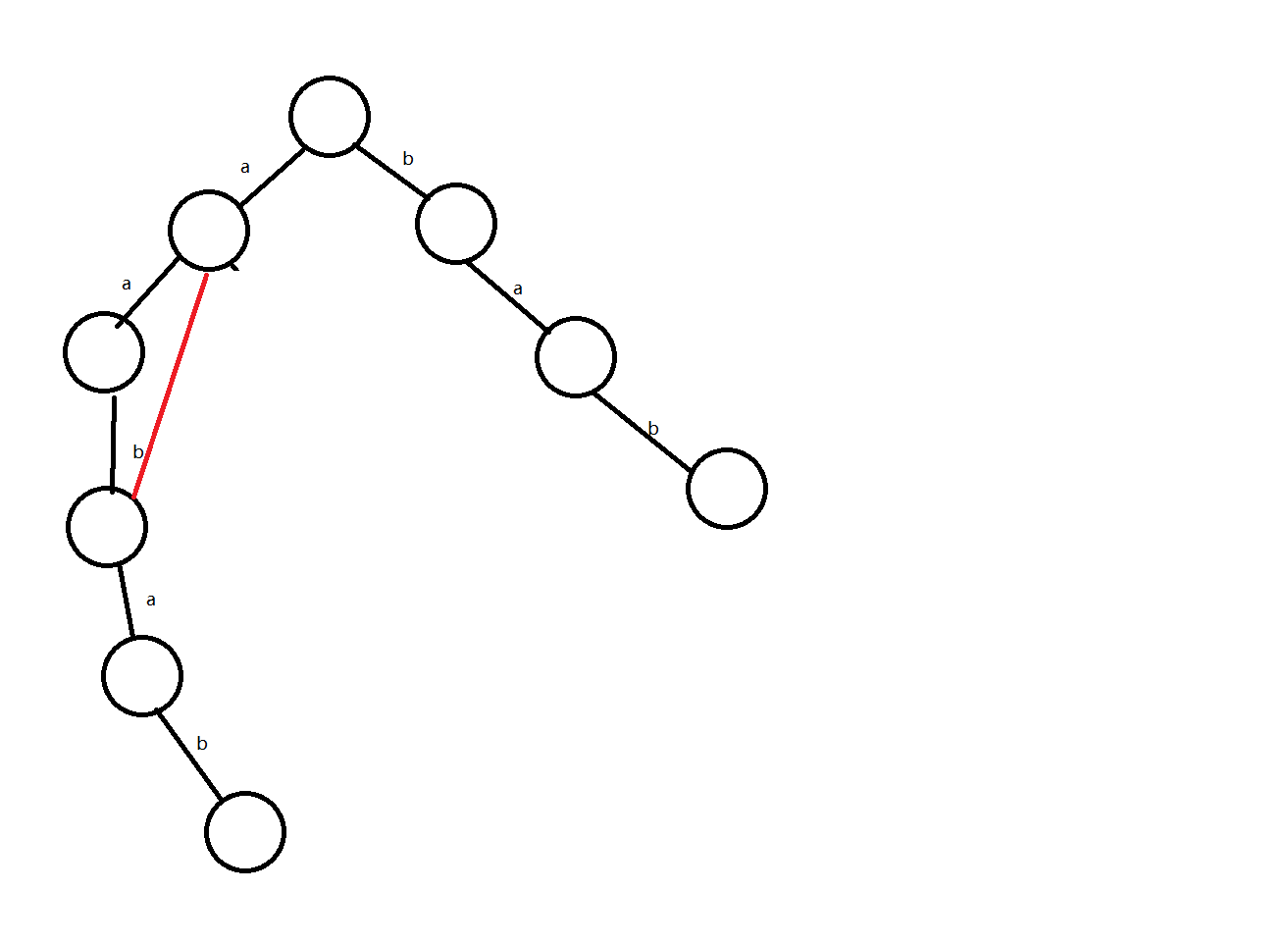
因此,我们想要找到一个节点数和边数尽可能少的DAG
2. 后缀自动机的构建
定义:我们定义endpos(a)表示a子串在整个string中出现的位置(只记录最右的位置)
例如对于string = “abbab”,下标对应12345 我的endpos(“ab”) = {2,5},endpos(“bab”) = {5}
现在可以证明三个结论
(1)如果两个子串的endpos相同,则其中一个子串一定是另一个的后缀
对于两个子串s,t,要求len(s) $\le$ len(t),那么如果我的s不是t的后缀,则会出现以下的情况
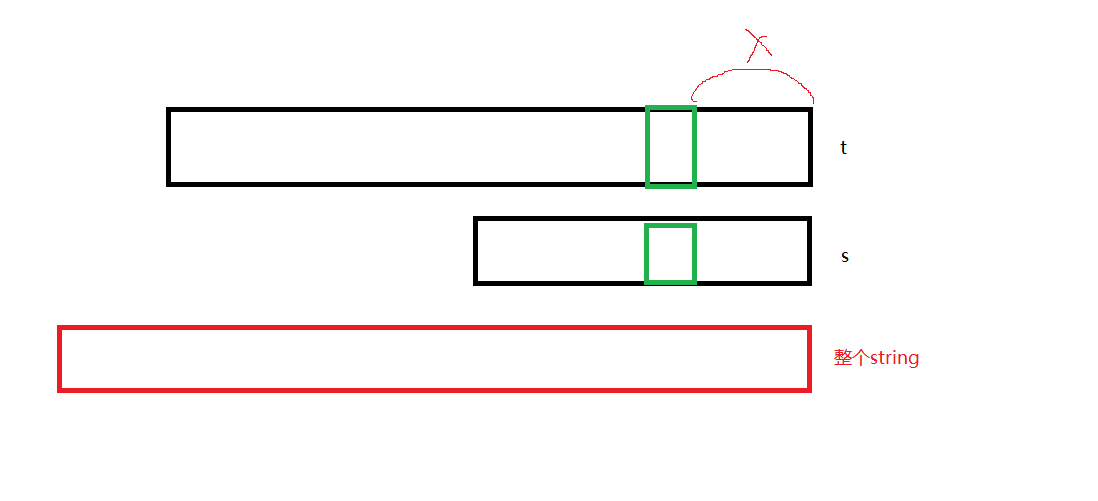
因为s不是t的后缀所以一定存在一个位置(绿色的位置)使得t[i]$\neq$s[i]
但是既然我的s与t的endpos相同,放在整个string串上来看t[i - x] = s[i - x],即绿色位置必然是相等的,与前提矛盾,所以反证法成立
(2)对于任意两个子串t,p满足len(t)$\le$len(s),要么endpos(t)$\subseteq$endpos(s),要么endpos(t)$\cap$endpos(s) = $\emptyset$
分为两种情况来讨论:
case1:t是s的后缀,则显然有endpos(t)$\subseteq$endpos(s)
case2 :t不是s的后缀,根据我的推论1,两个子串的endpos必然不同,即endpos(t)$\cap$endpos(s) = $\emptyset$
(3)对于endpos相同的子串,可以视作一个等价类,满足子串长度连续,且均为后缀
例如对于“aabab”,endpos=4的子串有aaba,aba,ba,a可以发现长度连续,且后一个为前一个的后缀
显然有长度覆盖的区间是连续的
对于后缀结论,通过推论2,可得:endpos(t)$\subseteq$endpos(s)$\Rightarrow$t是s的后缀
(4)endpos的等价类个数有$O(n)$个
对于一个类,我一定能从中找到一个长度最长的字符串s,此时我在s前加上一个字符,记作newstr
那么此时我的newstr一定不存在我的endpos=endpos(s)所代表的string集合中,因此得到了一个新的等价类,但是我的endpos(newstr)$\subset$endpos(s)
如果我在s前加上两个不相同的字符(记作str2)呢?显然此时有endpos(str2)$\cap$endpos(newstr)=$\emptyset$,因此我的str2和newstr分别代表的等价类可以视作endpos(s)的划分,不会超过原有集合的大小,因此所有的等价类加在一起不会超过$2|endpos(s)|$个,因此可以视作是$O(n)$的
此时给出如下定义:若集合B是我集合A的一个划分,则称A是B的父亲
(5)一个等价类a,称最长的子串为len(a),最短的子串为minlen(a),设fa(a)表示类a的父亲,有len(fa(a)) + 1 = minlen(a)
这是显然的,因为我在endpos(a)的最长str前加上一个字符,得到的endpos记作b,根据推论4,fa(b) = a,且此时的c + strZ一定是集合b中最短的str
此时我们可以尝试给出aababa的后缀自动机形式了(图中节点旁边写的str代表该endpos集合包含的最长str)
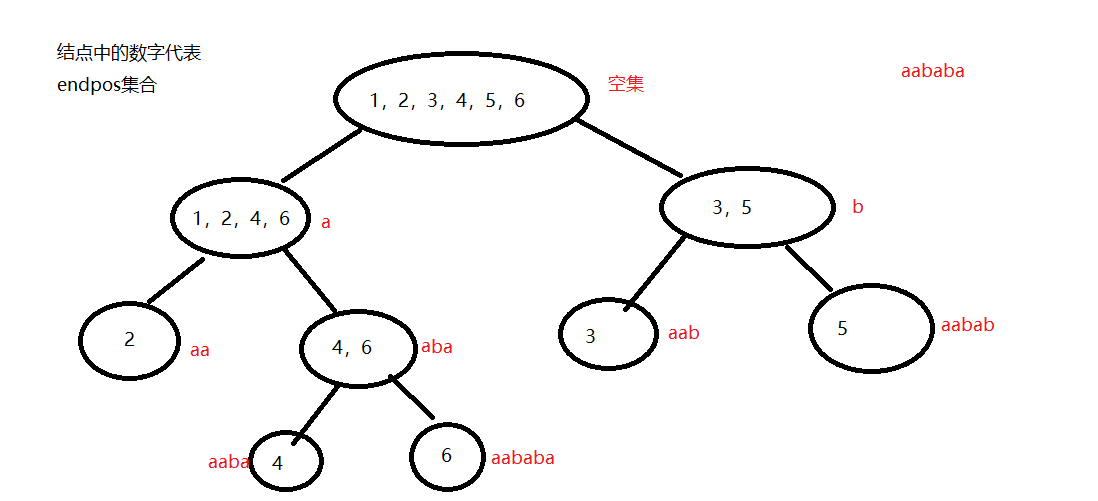
后缀自动机的最终形态并不是如此,还需要加上边,使得从源点出发到节点i的任意一条路径形成的字符串都是属于i的等价类
图中黑色的线代表的是parent tree的边,蓝色的线是后缀自动机的边
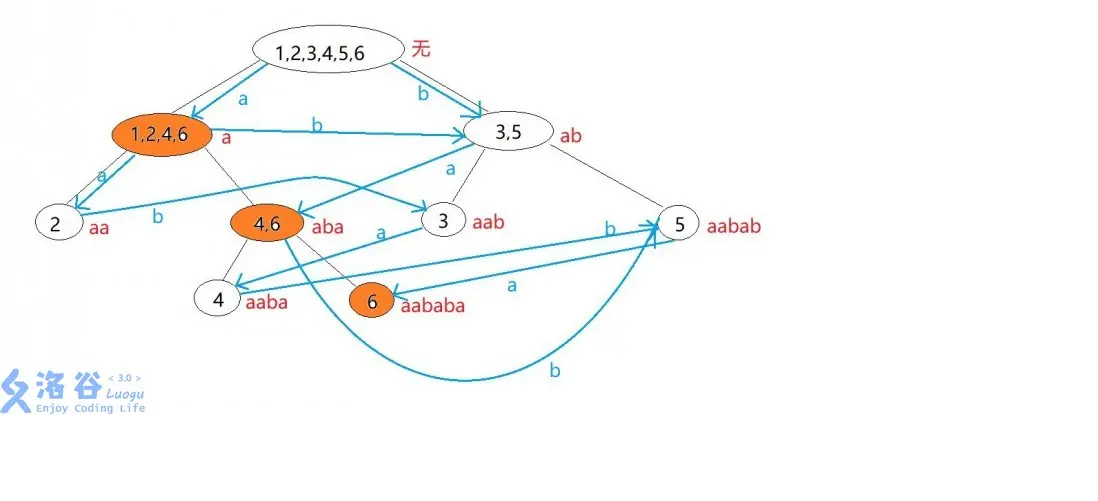
我们可以理解为沿着parent tree的边跑,相当于在字符串前面添加字符,而沿着后缀自动机的边跑,相当于在字符串后面添加字符