后缀数组SA

后缀数组

1. 后缀数组用来解决什么问题

​ 对于一个str，我们设$suf(x)$表示str从x位置开始的后缀，例如str=“abababa“,则$suf(3)=ababa$

​ 另外我们定义$lcp(suf_i,suf_j)$表示i和j两个字符串的最长公共前缀

​ 要求我们把后缀$suf(1),suf(2),……,suf(n)$按照字典序从小到大排序好，得到一个后缀数组

2. 如何得到后缀数组

方法1： 暴力sort

​ 对于一个str，我们有n个后缀，利用sort暴力排序，一共有n个后缀，每次比较的复杂度时$O(n)$，最终复杂度是$O(n^2\log n)$

方法2： 二分lcp+Hash

​ 对于任意两个后缀$suf(i)和suf(j)$，我们利用二分和哈希得到他们的lcp，比较他们两个的大小只需要比较lcp后的第一个位置即可。这样的复杂度是$O(\log n)$，总复杂度是$O(n\log^2n)$

方法3： 倍增做法

​ 我们定义$sa[i]$表示排名为i的后缀的开始位置，$rank[i]$表示后缀$suf(i)$的排名。显然有如下结论：$sa[rank[i]] = i$，$rank[sa[i]] = i$，即sa和rank互为反函数

​ 定义$sub[i][k]$表示str从i开始长度为k的子串(若长度超过了str的范围，则之后的都视为空)。$rank[i][k]$表示$sub[i][k]$在所有长度为$2^k$的子串中的排名，$sa[i][k]$表示所有长度为$2^k$的子串中，排名为i的子串是从哪里开始的

​ step1：首先求出所有$sub[1][0],sub[2][0],……,sub[n][0]$的字典排序

​ step2：求出所有$sub[1][1],sub[2][1],……,sub[n][1]$的字典排序

​ ……

​ 当子串长度$2^k>n$时，子串的排序就是我的后缀排序（一共做$\lceil \log k\rceil$次）

​ 那么我们如何快速的求出$sub[1][k+1],sub[2][k+1],……,sub[n][k+1]$的字典排序呢？利用$sub[1][k],sub[2][k],……,sub[n][k]$的结果

​ 对于$sub[i][k+1]和sub[j][k+1]$我们可以分成两部分来比较，第一部分是$sub[i][k]和sub[j][k]$，第二部分是$sub[i+2^k-1][k]和sub[j+2^k-1][k]$

​ 如果两者第一部分就不同，那么我们根据$rank[i][k]和rank[j][k]$就可以判断两者的大小

​ 如果第一部分相同，就根据$rank[i+2^k-1][k]和rank[j+2^k-1][k]$比较两者的大小

​ 如果把这两部分看成是pair的话，就是比较$\{rank[i][k],rank[i+2^k-1][k] \}和\{rank[j[k],rank[j+2^k-1][k] \}$，当然这里有一个显而易见的优化，我的$rank[i][k+1]$和$sa[i][k+1]$只和$rank[i][k]和rank[j][k]$有关，所以可以使用滚动数组

​ 这里我们利用基数排序来比较他们的大小，对于基数排序来说，需要先比较second再比较first

​ 于是有如下代码:

先对second进行排序

for (i = 1; i <= n; ++i) ++cnt[rk[id[i] + w]];	//w代表2^k,id[i]表示我之前的sa[i]
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[id[i] + w]]--] = id[i];	//注意这里需要倒序

再对first进行排序

for (i = 1; i <= n; ++i) ++cnt[rk[id[i]]];	//同理这里的id[i]就是我之前的sa[i]
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[id[i]]]--] = id[i];	//同理这里也需要倒序

最后把我的结果转移到新的rank中，对于排序后相邻的两个sub，如果他们的first和second都相等，那他们更新后的rank也相等

for (p = 0, i = 1; i <= n; ++i) {
	if (oldrk[sa[i]] == oldrk[sa[i - 1]] &&	//这里的oldrk[i]表示我之前的rank[i]
		oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) {
        rk[sa[i]] = p;
    } else {
       	rk[sa[i]] = ++p;
    }
}

倍增算法的一点优化

1.第二关键字无需基数排序

​ 第二关键字排序的实质，其实就是把对于$sa[i]+w>n$的后缀，放到id的头部，因为前后两次唯一会产生变化次序的位置，就是我满足$sa[i]+w>n$的所有i。在$len=w/2$时，他们的第二关键字>0，在$len=w$时，他们的第二关键字=0。

​ 因此得到如下的代码

int cur = 0;
for (int i = n - w + 1; i <= n; i++) id[++cur] = i;
for (int i = 1; i <= n; i++)
  	if (sa[i] > w) id[++cur] = sa[i] - w;

2.值域的优化

​ 一开始我们利用的是ascall码作为值域，事实上值域不需要这么大，利用我们最后合并时得到的不同种类p即可

3. 若排名不同可以直接输出后缀数组

​ 当种类(p) = 字符串的长度(n)时，后缀数组其实已经排好了，直接输出即可

所以综上优化，得到我的后缀数组的模板

for (int i = 1; i <= n; i++) cnt[rk[i] = s[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--) sa[cnt[rk[i]]--] = i;

for (int w = 1;; w <<= 1, m = p) {  // m = p 即为值域优化
    int cur = 0;
    for (int i = n - w + 1; i <= n; i++) id[++cur] = i;
    for (int i = 1; i <= n; i++)
      	if (sa[i] > w) id[++cur] = sa[i] - w;

    memset(cnt, 0, sizeof(cnt));
    for (int i = 1; i <= n; i++) cnt[rk[i]]++;
    for (int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];
    for (int i = n; i >= 1; i--) sa[cnt[rk[id[i]]]--] = id[i];

    p = 0;
    memcpy(oldrk, rk, sizeof(oldrk));
    for (int i = 1; i <= n; i++) {
      if (oldrk[sa[i]] == oldrk[sa[i - 1]] &&
          oldrk[sa[i] + w] == oldrk[sa[i - 1] + w])
        rk[sa[i]] = p;
      else
        rk[sa[i]] = ++p;
    }

    if (p == n) break;  // p = n 时无需再排序
}

2. 利用后缀数组，得到两个后缀的lcp

我们定义$height[i]=lcp(suf_{sa[i-1]},suf_{sa[i]})$值得注意的是，这里的两个后缀的后缀数组sa中相邻的两个

那如果我想得到任意的两个后缀的lcp呢？有结论

$lcp(suf_i,suf_j)=min_{k=l+1}^{r}(height[k])$，其中$l=sa[suf_i],r=sa[suf_j]$，这里可以维护一个RMQ实现

证明：

​ 首先证明对于$s1<s2<s3有lcp(s1,s3)=min(lcp(s1,s2),lcp(s2,s3))$

以下图中的黑色代表$lcp(s_1,s_2)$红色代表$lcp(s_2,s_3)$

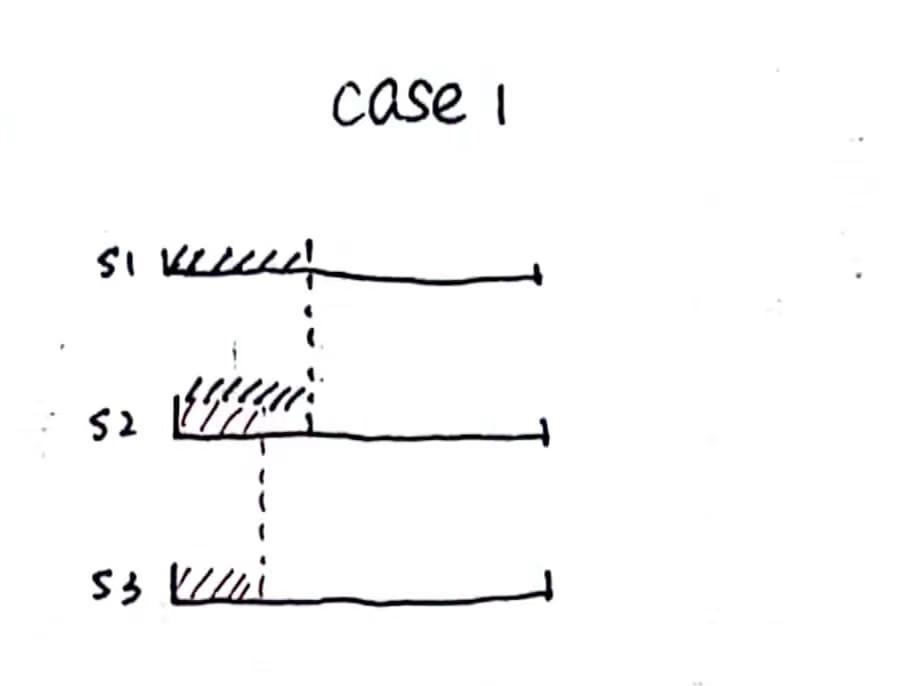
对于这种情况显然成立，假设说我的$lcp(s_1,s_3)>lcp(s_2,s_3)$，则有$s_3[i+1]\ne s_2[i+1],s_3[i+1]=s_1[i+1]\rightarrow s_1[i+1] \ne s_2[i+1]$，与我的假设矛盾

同理以上case1的情况，也能得到结论成立

当我三个长度都相等的时候，如果说此时$lcp(s_1,s_3)>lcp(s_2,s_3)$那么，就有$b\ne c \land b\ne a$，那么此时我的$s_1,s_2,s_3$的排序就不是这样的，应该是$s_1,s_3,s_2,即s_2不会在s_1,s_3之间$，故假设矛盾。

综上我们的结论成立。

​ 之后再从s1,s3之间找出所有的$s_i$都满足$lcp(s1,s3)=min(lcp(s_1,s_i),lcp(s_i,s_3))$，即可得证。(不严格的证明)

​

那么如何快速求解height，有结论

$height[l]\ge height[r]-1,其中l=rank[i],r=rank[i-1]$

不会证明，记住就行

有如下代码，求height

for (i = 1, k = 0; i <= n; ++i) {
  if (rk[i] == 0) continue;
  if (k) --k;
  while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
  height[rk[i]] = k;
}

​

​