树型DP
选择节点类的题目
例1. 没有上司的舞会
原题链接
解:我们设$dp[i][0/1]$分别表示 选/不选 第$i$个人的最大快乐值,设当前节点为u,u的儿子为v,$a[i]$表示i的快乐值
那么,我们可以列出他的转移方程:
$\begin{cases} \begin{aligned} dp[u][0] &=\sum \max{(dp[v][0],dp[v][1])} \\ dp[u][1] &=\sum \max{(dp[v][0],dp[v][1])+a[u]} \end{aligned} \end{cases}$
我们利用dfs的方式即可实现功能
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| int dfs(int u, int ok) {
if (dp[u][ok] != LONG_LONG_MIN) {
return dp[u][ok];
}
if (!ok) {
int ans = 0;
for (auto &it : edge[u]) {
ans += dfs(it, 1);
}
return dp[u][ok] = ans;
} else {
int ans = 0;
for (auto &it : edge[u]) {
ans += dfs(it, 1);
}
int ans2 = r[u];
for (auto &it : edge[u]) {
ans2 += dfs(it, 0);
}
return dp[u][ok] = max(ans, ans2);
}
}
|
树上背包问题
例1. 有线电视网
原题链接
解:我们设$dp[i][j]$表示以i为根的子树中,满足j个人需求的最大利润。其中第$i$条边的成本为$c[i]$,第i个人愿意交的钱为$a[i]$,$cost[i][j]$表示从i到j的成本
那么我们怎么去求$dp[u][j]$呢?首先我们肯定要遍历u的所有儿子v,但是对于不同的v,我们可以选择不同的$dp[v][j’]$,来使得我的$dp[u][j]$最大。很显然,任意的$dp[v][j’]$是已知的,所以这道题就变成了一道背包问题,即已知背包容量为j,我有若干个物品,价值为$dp[v][j’]$,重量为$j’$。
1
2
3
4
5
6
7
8
9
10
11
| void dfs(int u) {
if (leaf[u]) return ;
for (auto &it : edge[u]) dfs(it), siz[u] += siz[it];
for (auto &it : edge[u]) {
for (int j = siz[u];j >= 1;j--) {
for (int k = 1;k <= siz[u];k++) {
dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[it][k] - cost[u][it]);
}
}
}
}
|
为什么以上代码需要我记录$siz[u]$,因为对于以i为根的子树,他最多也就能满足$siz[i]$个人
例2. 树上染色
原题链接
解:我们设$dp[i][j]$表示以i为根的子树中染了j个黑色的点,对答案的贡献。一共要涂m个黑点
由此我们可以列出状态转移方程,对于从u到v的路径 ,长度为w,有$dp[u][j]=\max(\sum dp[v][j’]+tot*w)$
其中我的tot表示,w对答案的贡献,其中$tot=j(m-j)+(siz[v]-j)(n-siz[v]+j-m)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| void dfs(int u, int pre) {
siz[u] = 1, dp[u][0] = dp[u][1] = 0;
for (int i = head[u];i;i = e[i].nxt) {
int v = e[i].to, weight = e[i].weight;
if (v == pre) continue;
dfs(v, u);
siz[u] += siz[v];
for (int j = min(m, siz[u]);j >= 0;j--) {
for (int k = 0;k <= min(j, siz[v]);k++) {
if (dp[v][k] == -1 || dp[u][j - k] == -1) continue;
int tot = k * (m - k) + (siz[v] - k) * (n - m - siz[v] + k);
dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[v][k] + tot * weight);
}
}
}
}
|
换根DP
例1. STA-station
原题链接
解:设$dp[i]$表示以i为根的时候,深度和是多少。
对于换根DP来说,一般都需要dfs两遍,例如在本题中,第一次dfs,能够求出以1为根的深度和,即$dp[1]$
第二次dfs时,从以u为根到以v为根,如下图所示:
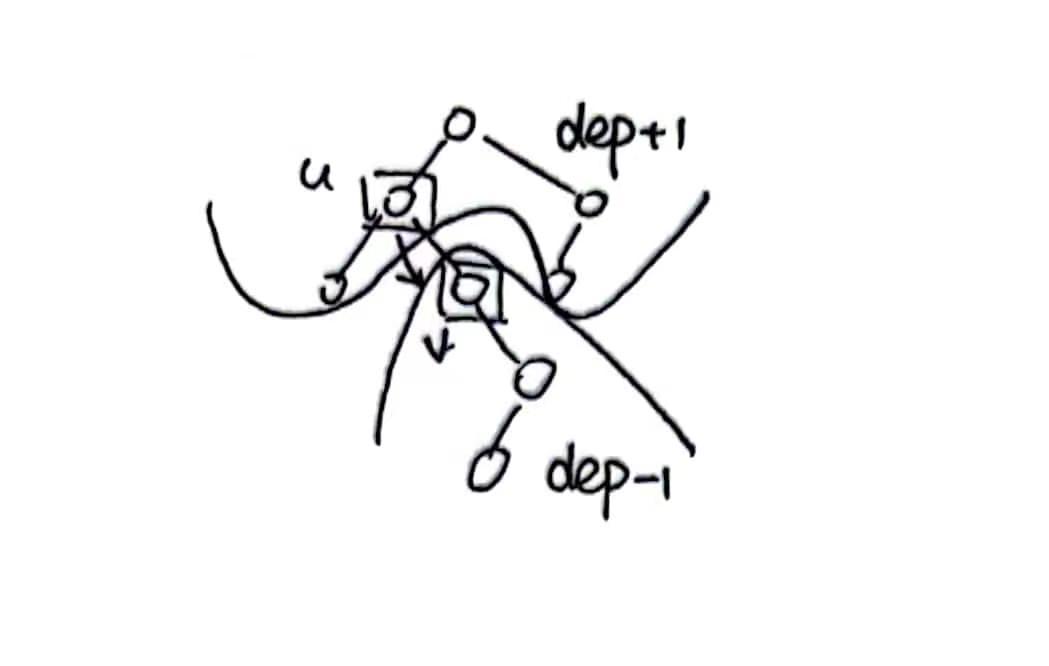
我们可以看到对于v的子树,他的dep都是-1,其余的dep都是+1
所以$dp[v]=dp[u]-(n-siz[v])+siz[v]=dp[u]+2*siz[v]-n$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void dfs(int u, int pre) {
for (auto &it : edge[u]) {
if (it == pre) continue;
dep[it] = dep[u] + 1;
dfs(it, u);
siz[u] += siz[it];
}
}
void DP(int u, int pre) {
for (auto &it : edge[u]) {
if (it == pre) continue;
dp[it] = dp[u] + (n - siz[it]) - siz[it];
if (dp[it] > ans) ans = dp[it], idx = it;
DP(it, u);
}
}
|
