牛客多校1

牛客暑假多校第一场解题报告

比赛链接

A. A Bit Common

原题链接

题目大意：对于一个序列A（每个数都$\lt 2^m$），存在一个子序列B，使得$AND_{i \in B}B_i=1$，则被计数，问一共有几个这样的序列A，允许有重复数字

解：我们先钦定有序列A的长度是k，那么这k个数一定都是奇数，换句话说他们二进制的最后一位一定是1，现在考虑前面的$m-1$位，显然，如果我想让他们的AND和是1的话，这$m-1$位一定至少有一个0，所以一共有$\binom{n}{k}\times (2^k-1)^{m-1}$。

解释一下，$2^k$表示我第i位任意选的情况总数，$2^k-1$表示从这所有的情况中去除全部为1的情况。

接着我们再去考虑其余$n-k$个数，他们最后一位一定是0，所以他们无论怎么AND，一定不会得到结果1，所以其余的数只要最后一位是0即可，前面$m-1$位任取，一共有方案数$2^{(m-1)\times(n-k)}$

cin >> n >> m >> mod;
   int co = 1, ans = 0;
   for (int i = 0;i <= n;i++) {
       a[i][0] = a[i][i] = 1;
       for (int j = 1;j < i;j++) {
           a[i][j] = (a[i - 1][j - 1] + a[i - 1][j]) % mod;
       }
   }
   for (int k = 1;k <= n;k++) {
       // co = ((co * (n - k + 1) % mod) % mod * inv % mod) % mod;
       int co = a[n][k];
       int res1 = (qpow(2, k) - 1 + mod) % mod, res2 = qpow(res1, m - 1), 
           res3 = qpow(2, m - 1), res4 = qpow(res3, n - k);
       ans = (ans + co * res2 % mod * res4 % mod) % mod;
   }
   cout << ans << endl;

B. A Bit More Common

原题链接

题目大意：与A题不同的是，这道题目要求序列A存在至少两个子序列B，使得$AND_{i\in B}B_i = 1$

解：承接第一道题目的思路，我们在A题中已经得到存在至少一个子序列的个数了，是不是只需要减去存在严格等于1的方案数，剩下来的就是我B的方案数。

那么我该怎么算出这些严格等于1的方案数呢？

我们给出以下定义：如果某一位的数字中只有一个0，那么这位数就是不可或缺的，我们称这样的位为特殊位。注意：这里我们不讨论这$i$个数具体是什么，只谈论这一位的数字分布情况，当然了，我们讨论的前提都是这个序列A满足$AND_{i\in A}A_i=1$。

显然，如果一个序列A只有一个子序列AND=0，则序列A中的每一个数字都至少都对应这一个特殊位：因为如果某一个数字对应两个及以上的特殊位的话，这个数字完全可以被删去，不符合我们的定义。

我们设$dp[i][j]$表示$i$个数字对应$j$个特殊位有几种方案数。有如下转移$dp[i][j]= i \times(dp[i][j-1]+dp[i-1][j-1])$。

为什么呢？如下图（图片里下标好像写错了，是从1开始的，而不是0）：

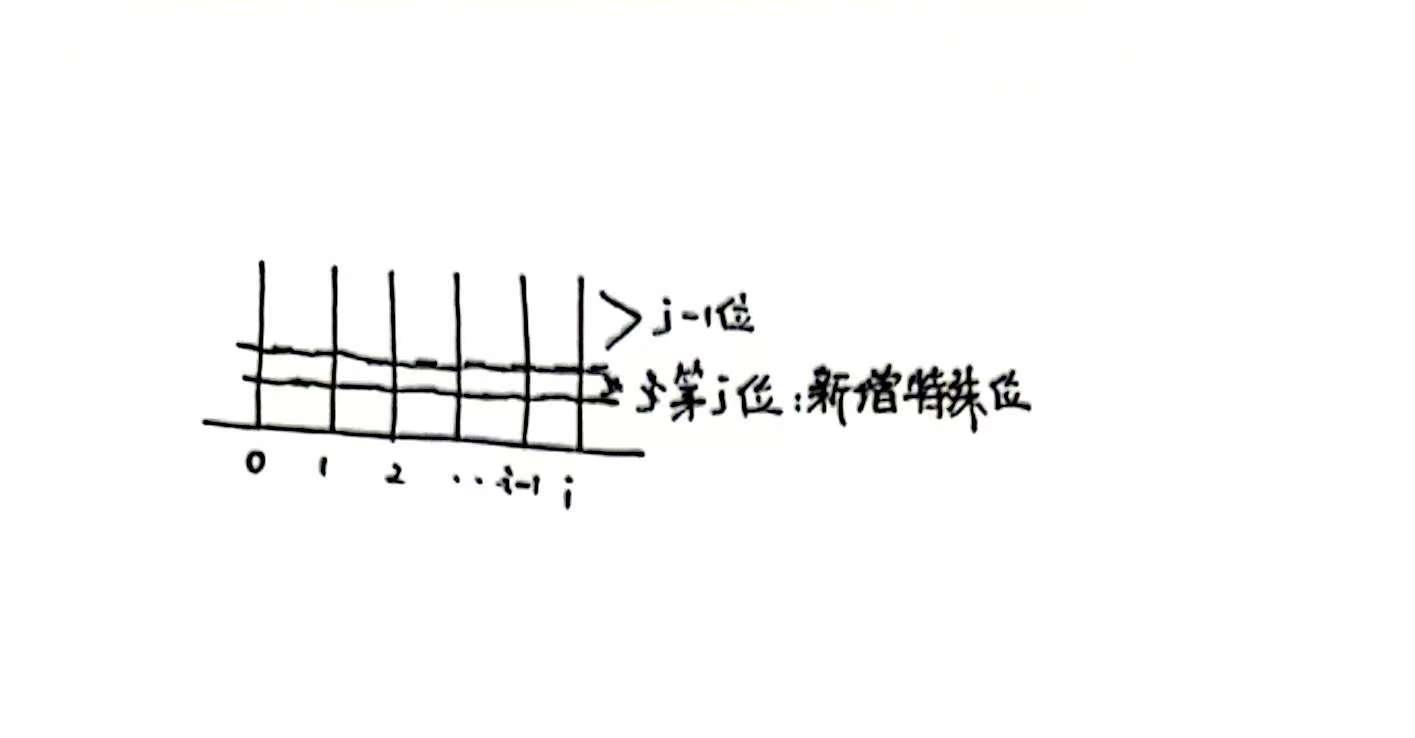
对于从$dp[i][j-1]$转移过来的情况，我的第j位可以在i个数中任选一个，有贡献$i\times dp[i][j-1]$

对于从$dp[i-1][j-1]$转移过来的情况（此时我们认为新增的特殊位就在i上），我新增的数可以放在任意一个位置上，所以也有贡献$i\times dp[i1-][j-1]$

最后可以求得严格等于1的方案数为$\sum_{i=k}^{m-1} \binom{m-1}{i}(2^k-k-1)^{m-1-k}dp[k][i]$

最后的答案就是A的答案减去严格等于1的答案。

NOTE：用板子会快一点。

D. XOR of Suffix Sums

原题链接

题目大意：在线查询数组后缀和的异或和

解：这个模数十分特别刚好是$2^{21}$，所以暗示我们可以按位维护我要的答案。

一个后缀可以转换为两个前缀和的差，有$sum[n]-sum[i-1]=suf[i]$，因此这道题目需要我们维护一个值域树状数组，维护的值域都是$-sum[i]$，其中$-sum[n]$不会在树状数组中维护。

现在我想要知道第$d$位一共有奇数个还是偶数个1，观察可得如下结论：若$sum[n]-sum[i-1] \mod{2^{d+1}} \ge 2^{d}$则$sum[i-1]$在$d$位贡献了1，我们可以利用这个式子得到如下结论：

$2^{d+1} \gt (sum[n]-x) \mod{2^{d+1}} \ge2^d \\ \Rightarrow 2^{d+1} - sum[n] \mod{2^{d+1}} \gt -x \ge 2^d-sum[n] \mod{2^{d+1}}$

得到了我要查询的x所在的上下界，分别是$l=2^d-sum[n] \mod{2^{d+1}},\quad r=2^{d+1}-sum[n] \mod{2^{d+1}}$

当我的$l \le r$时，正常查询，当我的$r \lt l$时需要查询$[0,r]\cup[l,2^{d+1}]$。为什么，可以理解为因为有取模的存在导致原本在$l$后面的$r$重新出现在了$l$的前面，这是$[r+ 1,l -1]$的区间是不用查询的。

int q;
   cin >> q;
   while (q --) {
       int t, v;   cin >> t >> v;
       while (t--) {
           for (int i = 0, mod;i <= 20;i++) {
               mod = 1 << (i + 1);
               tr[i].update((mod - sum[n - 1] % mod) % mod, -1);
           }
           n --;
       }       
       n ++; sum[n] = (sum[n - 1] + v) % MOD;
       for (int i = 0, mod;i <= 20;i++) {
           mod = 1 << (i + 1);
           tr[i].update((mod - sum[n - 1] % mod + mod) % mod, 1);
       }
       int ans = 0;
       for (int i = 0, cnt = 0;i <= 20;i++) {
           int mod = 1 << (i + 1), tmp = 1 << i;
           int l = ((tmp - sum[n] % mod) + mod) % mod;
           int r = ((mod - sum[n] % mod) - 1 + mod) % mod; 
           if (l <= r) {
               cnt = tr[i].query(l, r);
           } else {
               cnt = tr[i].query(0, r) + tr[i].query(l, mod);
           }
           if (cnt & 1) ans |= (1 << i);
       }
       cout << ans << endl;
   }